JustGRPO深度解析:为何极简主义是扩散语言模型推理的关键
type
status
date
slug
summary
tags
category
icon
password
网址
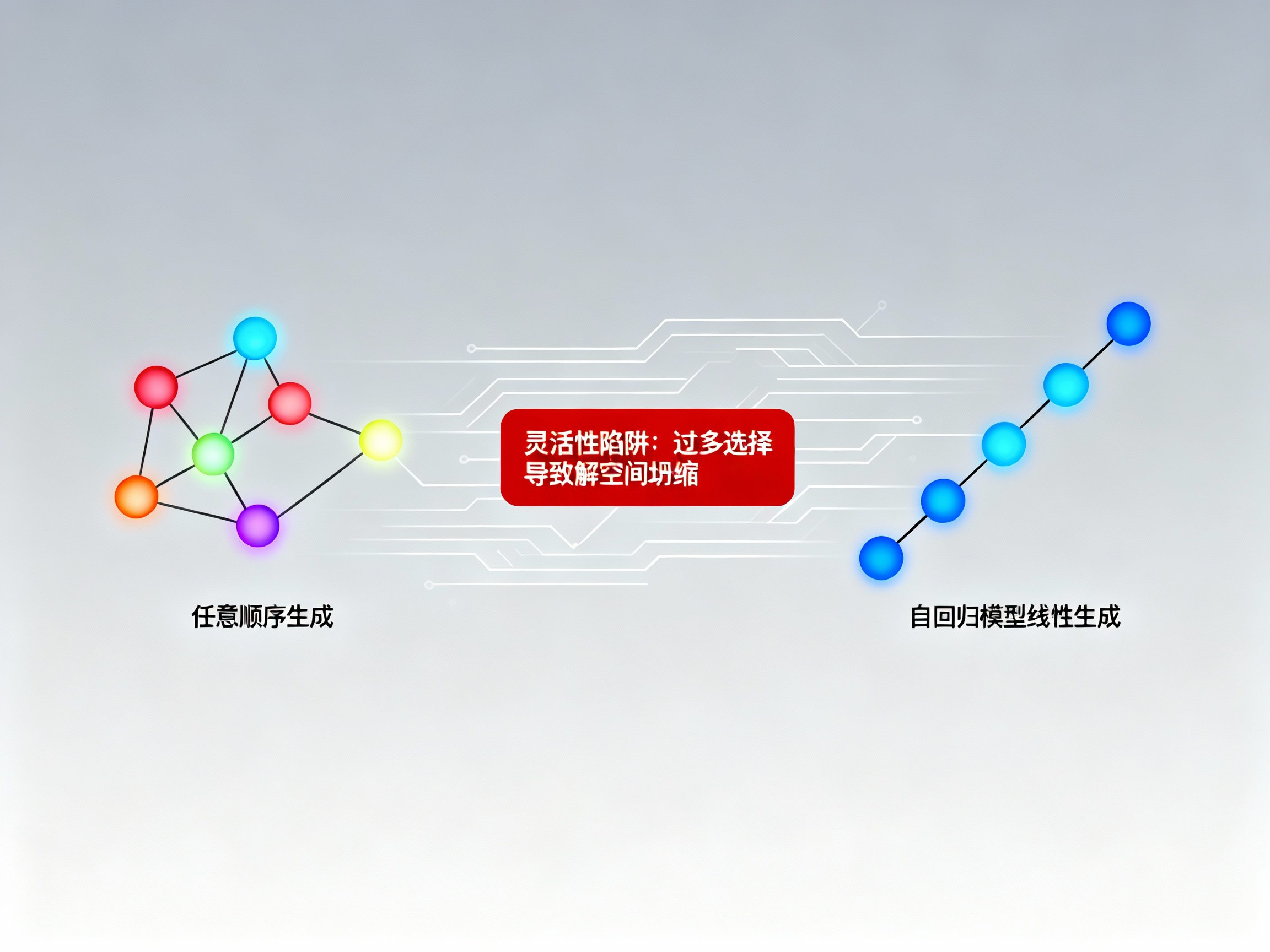
在当前的人工智能与大模型(LLM)研究领域,扩散语言模型(Diffusion LLMs, dLLMs)凭借其“任意顺序生成”和高效的并行解码能力,被视为挑战传统自回归(AR)模型地位的有力竞争者。直觉上,打破从左到右的线性束缚,应该能为模型提供更广阔的解空间,从而在数学推理和代码编写等复杂任务中释放更强的潜力。
然而,最新的研究成果《The Flexibility Trap》却揭示了一个令人意外的真相:这种看似优越的“灵活性”反而成为了限制模型推理能力的陷阱。为了解决这一问题,研究者提出了JustGRPO——一种回归极简主义的训练方法,通过在强化学习阶段重新引入自回归约束,成功解锁了扩散模型更深层次的推理性能。
灵活性陷阱:当自由成为负担
扩散语言模型的核心优势在于其生成的灵活性,即模型可以根据词项的置信度,在序列的任何位置优先填入内容。但研究发现,这种“任意顺序”在处理高难度推理任务时表现并不理想。
通过核心衡量指标 Pass@k(即在k次采样中至少获得一个正确答案的概率)的对比实验发现,虽然任意顺序在单次生成(k=1)时表现尚可,但随着采样次数k的增加,其性能提升速度远低于传统的自回归(AR)顺序。这意味着,在受限的AR顺序下,模型反而能够覆盖更广阔、更深层的正确解空间。这种现象挑战了我们对“自由度”的认知:在LLM推理中,过多的选择路径可能导致模型迷失方向。
熵降级现象:被跳过的逻辑关键点
为什么受限的AR顺序反而更强?研究者通过观察模型在生成过程中的行为,发现了所谓的“熵降级”(Entropy Degradation)现象。
在任意顺序模式下,模型拥有“避重就轻”的特权。当遇到不确定的逻辑转折点(如“Therefore”、“Thus”等衔接词)时,模型往往会跳过这些高难度的决策点,转而填充后面更容易确定的上下文。统计显示,这些被跳过的逻辑衔接词在解码时的熵(Entropy)显著低于自回归顺序。
在人工智能的逻辑推演中,这些衔接词往往是通往不同推理路径的“分叉口”。保持这些词的高熵状态,对于模型探索多样化的正确解至关重要。任意顺序下的“局部贪婪优化”虽然让单次生成看起来通顺,却导致了解空间的过早坍缩,牺牲了复杂推理的成功率。
JustGRPO:回归极简的强化学习方案
针对上述问题,JustGRPO 提出了一种返璞归真的策略。它不再试图为扩散模型设计复杂的、兼容任意顺序的强化学习算法,而是直接在 RL 训练阶段强制模型回归到自回归(AR)顺序。
这种设计思路具有极简的魅力:
1. 确定性轨迹:强制 AR 顺序使得强化学习过程中的信用分配(Credit Assignment)更加清晰。
2. 算法复用:可以直接利用成熟的 GRPO(Group Relative Policy Optimization)算法进行优化,无需额外的近似处理。
3. 直面不确定性:迫使模型在生成每一个 Token 时都必须面对当前的逻辑决策,从而学习到更稳健的联合概率分布。
在AI资讯界,这种“以退为进”的策略往往能带来意想不到的突破。
性能飞跃:推理增强与并行优势的共存
实验数据证明了 JustGRPO 的卓越表现。在数学推理基准测试 GSM8K 和 MATH-500 上,采用 JustGRPO 训练后的模型准确率分别达到了 89.8% 和 45.2%,显著超越了此前针对 dLLM 设计的各种复杂 RL 算法。在代码生成任务(HumanEval 和 MBPP)中,同样展现了极强的竞技力。
更令人振奋的是,这种训练方式实现了“训练约束”与“推理加速”的完美平衡。虽然在训练时限制了顺序,但模型本身的双向注意力机制并未受损。在推理阶段,模型依然可以无损地使用并行解码技术。
甚至在并行采样时,经过 JustGRPO 训练的模型表现出了更好的鲁棒性。在 MBPP 数据集上,当每步并行生成 5 个 Token 时,其相对于基座模型的领先优势进一步扩大。这说明模型学到了更高质量的语言规律,能够更好地容忍并行解码带来的近似误差。
总结与未来展望
JustGRPO 的成功为大模型的研究提供了一个深刻的启示:在追求模型架构的灵活性时,不能忽视训练过程中的约束价值。通过回归极简的自回归训练路径,我们不仅能够显著提升扩散语言模型的推理上限,还能保留其高效并行的原生优势。
随着 AGI 进程的加速,如何更有效地激发非自回归模型的潜力将成为热门课题。如果你想了解更多关于 AI新闻、Prompt 优化或 LLM 的前沿技术,欢迎访问 AI门户 获取最新的 AI日报 和深度技术指南。
JustGRPO 不仅仅是一个算法的改进,它更代表了一种研究哲学:有时候,通往高性能的路径并非更加复杂,而是对本质规律的回归。
Loading...
.png?table=collection&id=1e16e373-c263-81c6-a9df-000bd9c77bef&t=1e16e373-c263-81c6-a9df-000bd9c77bef)